Big O & 時間複雜度 & 空間複雜度 介紹(Big O & Time Complexity & Space Complexity) | 資料結構&演算法

時間和空間複雜度對於開發可擴展和高性能的程式碼影響深遠。我們將入門資料結構&演算法的世界,首先介紹 Big O 表示法,並演示如何分析和優化 JavaScript 程式碼,藉由改善程式的演算法來獲得更好的效能。
什麼是Big O:
Big O 表示法是一個數學概念,允許開發人員以輸入大小的增長率來表達演算法的效率。它側重於 最壞情況(Worst Case) 的分析。Big O 表示法不關心確切的運行時間,而是關心演算法的性能如何隨著輸入的增加而擴展。
例如,O(1)表示常數時間複雜度,表示演算法的執行時間保持一致,不管輸入大小如何。另一方面,O(n)表示線性時間複雜度,其中執行時間與輸入大小成線性增長。更複雜的表示法,如O(n^2)或O(log n),描述了不同的演算法效率模式。
Big O 時間複雜度:
時間複雜度分析有助於開發人員評估演算法的執行時間如何隨input的增加而增長。常見的 Big O 時間複雜度包括:
O(1) - 常數時間複雜度 :
- Constant (常數)
- 這表示演算法具有常數執行時間,不管輸入大小如何。一個例子是通過索引訪問陣列中的元素。
O(log n) - 對數時間複雜度 :
- Divide and Conquer (分而治之)
- 具有對數時間複雜度的演算法在每個步驟中減小問題大小,例如在排序陣列中進行二分查找。
O(n) - 線性時間複雜度 :
- Proportional (成比例成長)
- 在線性時間複雜度中,執行時間隨著輸入大小的增加而線性增長。遍歷陣列是O(n)複雜度的例子。
O(n log n) - 線性對數時間複雜度 :
- 這種複雜度常見於高效的排序演算法,如歸併排序和堆排序,它結合了線性和對數增長。
O(n^2) - 二次方時間複雜度 :
- Loop within a Loop (迴圈包裹迴圈)
- 具有二次方時間複雜度的演算法的執行時間與輸入大小的平方成正比。迴圈包裹迴圈是常見O(n^2)複雜度的例子。
Big O 空間複雜度:
空間複雜度測量演算法在執行期間使用的記憶體量與其輸入大小的關係。它有助於評估演算法在執行過程中如何有效地使用記憶體。常見的空間複雜度包括O(1)、O(n)、O(n^2)等。
O(1) - 常數空間複雜度 : 具有常數空間複雜度的演算法使用固定的記憶體量,不管輸入大小如何。
O(n) - 線性空間複雜度 : 線性空間複雜度表示使用的記憶體量隨著輸入大小的增加而線性增長。
通常來說,我們在JavaScript中考慮的Big O大多是討論時間複雜度
Big O 好壞 比較圖

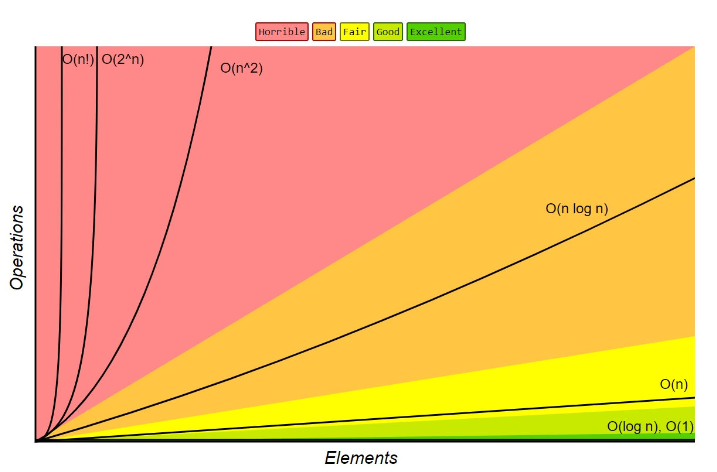
圖片參考來源devopedia
常見 資料結構&演算法 Big O 一覽表
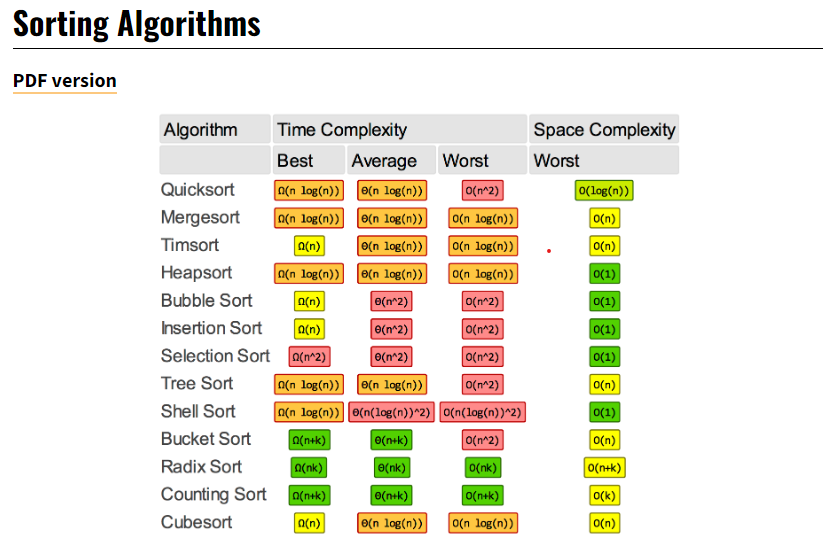
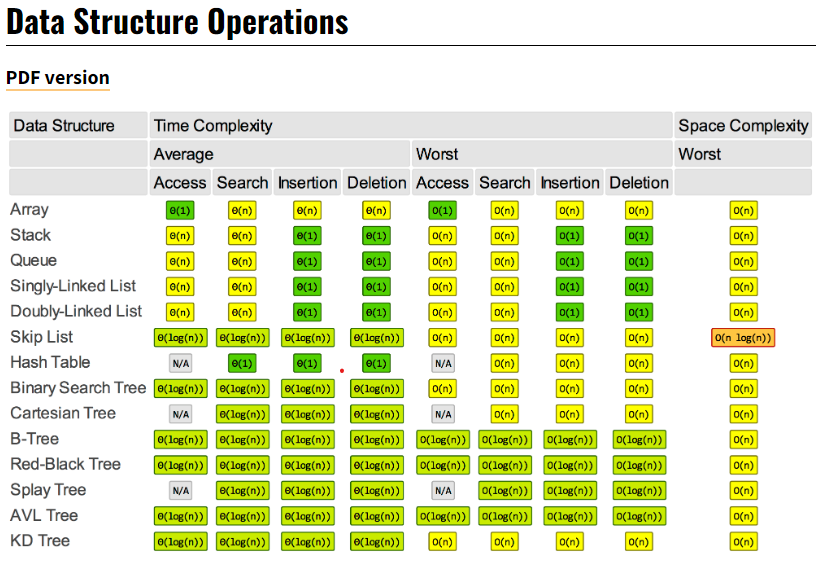
圖片參考來源weibeld.net
Tags